• un bouton aussi lourd que possible et qu’on peut enfiler sur un fil ou bien un écrou lourd

• du fil fin et résistant (longueur : 50 à 80 cm)

Sur un fil fin et résistant d’environ 50 centimètres de longueur, enfiler un bouton ou, mieux encore, un écrou d’acier aussi lourd que possible.

Il faut impérativement utiliser un objet à enfiler sur le fil pour que le fil puisse tourner par rapport à l’objet sans se tordre (un fil qui se tord freinerait le mouvement).

Sans tendre le fil, mettre l’écrou en rotation en faisant décrire des cercles à chacune des deux mains. on communique ainsi un mouvement circulaire au bouton retenu par le fil .

Lorsque l’écrou tourne suffisamment vite, arrêter de faire tourner les mains et tendre progressivement le fil.

L’écrou décrit des cercles de plus en plus petits, mais avec une vitesse angulaire de plus en plus grande.

L’écrou sur son fil constitue un système mécanique pseudo isolé.

Cela signifie que son moment cinétique se conserve au cours du temps.

Or celui-ci est proportionnel à la vitesse angulaire de rotation du boulon, ainsi qu’au carré du rayon de sa trajectoire.

Si on diminue le rayon du cercle en tirant sur le fil, la vitesse angulaire doit augmenter pour respecter la loi de conservation.

L’écrou tourne ainsi de plus en plus vite sur un cercle de rayon de plus en plus petit.

On peut considérer le fil comme pratiquement sans masse et le bouton comme un point matériel. Pour ces explications nous avons négligé le poids du bouton devant les autres forces en jeu car sa prise en compte aurait alourdi les calculs sans rien apporter à notre propos.

Lorsque les mains ne bougent plus, elles n’exercent aucune action pouvant modifier le moment cinétique du bouton qui reste donc constant.

Le moment cinétique 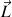du bouton est :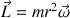

(c’est un vecteur constant)
(m : masse du bouton ; r : rayon du cercle décrit par le bouton ; 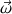vitesse angulaire du bouton).

Le rayon du cercle diminuant lorsqu’on écarte les mains et 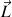restant constant, la vitesse angulaire ω augmente. Inversement, ω diminue lorsqu’on rapproche les mains, c’est-à-dire quand r augmente.